Khoảng tin cậy Wilson

Hàm wilsonScoreLowerBound() tính giá trị biên dưới của khoảng tin cậy Wilson cho một tỷ lệ thành công trong thống kê, thường được dùng để đánh giá xếp hạng hoặc xác suất với độ tin cậy cao mà không bị nhiễu bởi kích thước mẫu nhỏ.

✅ Mục đích:

• Tính một ước lượng thấp nhất đáng tin cậy cho tỷ lệ thành công $p = \frac{s}{n}$ với mức tin cậy (ví dụ 95%).
• Dùng trong: đánh giá sản phẩm, tỷ lệ bán hàng, xếp hạng (ranking), A/B testing, v.v.

📐 Giải thích toán học

1. Định nghĩa biến

• $s$: số lần thành công (successes)
• $n$: tổng số thử nghiệm (total trials)
• $p = \frac{s}{n}$: tỷ lệ thành công quan sát được
• $z$: giá trị Z tương ứng với mức độ tin cậy (95% → 1.96, 90% → 1.645)

2. Công thức toán học đầy đủ của Wilson Score Interval:

Đây là công thức khoảng tin cậy Wilson:

$$\text{CI} = \frac{p + \frac{z^2}{2n} \pm z \sqrt{ \frac{p(1-p) + \frac{z^2}{4n}}{n} }}{1 + \frac{z^2}{n}}$$

• $\pm$: cho phép tính cả biên dưới và biên trên
• Trong hàm này, ta chỉ tính biên dưới (lower bound)

3. Diễn giải từng phần:

4. Mã PHP tương ứng:

$p = $s / $n;                  // Tỷ lệ quan sát
$z2 = $z * $z;                 // z^2
$denominator = 1 + ($z2 / $n); // Mẫu số

$center = $p + $z2 / (2 * $n); // Tâm hiệu chỉnh
$margin = $z * sqrt(($p * (1 - $p) + $z2 / (4 * $n)) / $n); // Sai số

$score = ($center - $margin) / $denominator; // Biên dưới

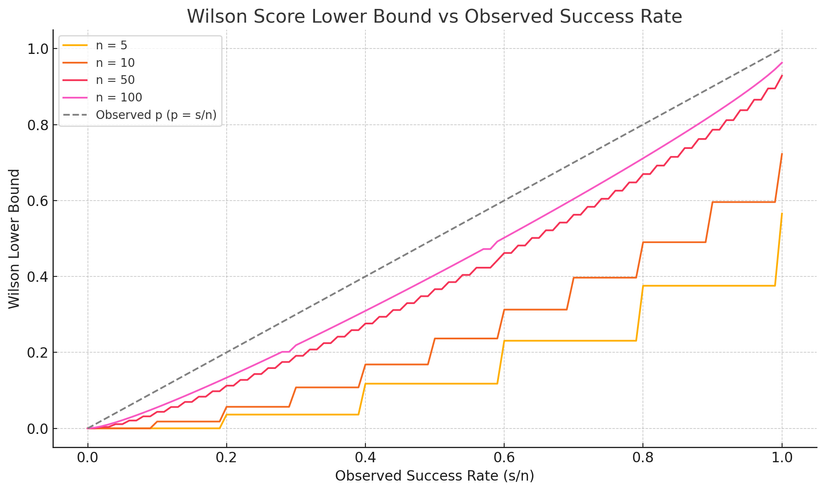
📊 Ví dụ minh họa

Giả sử:

• $s = 5$, $n = 10$
• $p = 0.5$
• $z = 1.96$ (95%)

Tính:

$$\text{Biên dưới} ≈ \frac{0.5 + \frac{1.96^2}{20} - 1.96 \cdot \sqrt{ \frac{0.5(1 - 0.5) + \frac{1.96^2}{40} }{10} }}{1 + \frac{1.96^2}{10}} \approx 0.236$$

→ Dù bạn thấy tỉ lệ là 50%, Wilson chỉ ước lượng thấp hơn (23.6%) để phòng trường hợp bị overfitting (mẫu nhỏ quá).

📌 So sánh với các cách khác

✅ Khi nào dùng Wilson Score?

• Khi bạn muốn:

  • Đánh giá tỷ lệ thành công với mức tin cậy cao.
  • So sánh ranking công bằng giữa các nhóm có mẫu nhỏ/lớn khác nhau.
  • Tránh bias do “ít dữ liệu mà tỷ lệ cao”.

Ví dụ:

• Sản phẩm A: bán được 1/1 → 100% (nhưng mẫu nhỏ)
• Sản phẩm B: bán được 20/40 → 50% → Wilson sẽ "phạt" sản phẩm A do độ tin cậy thấp.