Tờ Mờ Sáng học Lập trình @tmsanghoclaptrinh

7.4K 435 82

Đã đăng vào Thứ Ba, 3:32 SA 21 phút đọc

171

SERIES INDEX NÂNG CAO - BÀI 2: ĐÀO SÂU VÀO CÁC CẤU TRÚC DỮ LIỆU DÙNG ĐỂ LƯU TRỮ INDEX TRONG MYSQL

MayFest2025

Nếu anh em thấy hay thì ủng hộ tôi 1 follow + 1 upvote + 1 bookmark + 1 comment cho bài viết này tại Mayfest 2025 nhé. Còn nếu bài viết chưa hữu ích thì tôi cũng hi vọng anh em để lại những góp ý thẳng thắn để tôi có thể học hỏi và cải thiện kiến thức của mình. Cảm ơn anh em nhiều!

Đọc thêm các bài viết khác trong Series Index nâng cao: Kiến trúc và Tối ưu hóa Index trong MySQL dành cho Developer và DBA

Mục lục

1. Cấu trúc dữ liệu B-Tree. Phân tích chi tiết và hiểu ưu nhược điểm của nó
2. Cấu trúc dữ liệu R-Tree, Hash Index và Inverted List
- 2.1. Spatial Data Types sử dụng R-tree
- 2.2. MEMORY Table hỗ trợ Hash Index
- 2.3. InnoDB sử dụng Inverted List cho FULLTEXT Index
3. Kết luận

1. Cấu trúc dữ liệu B-Tree

Nếu các bạn đã từng đọc documentation của MySQL thì cũng sẽ thấy họ ghi rõ rằng:

"Most MySQL indexes (PRIMARY KEY, UNIQUE, INDEX, and FULLTEXT) are stored in B-trees. Exceptions: Indexes on spatial data types use R-trees; MEMORY tables also support hash indexes; InnoDB uses inverted lists for FULLTEXT indexes."

có nghĩa là:

Hầu hết các index trong MySQL (ví dụ như PRIMARY KEY, UNIQUE, INDEX, FULLTEXT) sử dụng cấu trúc dữ liệu B-Tree để lưu trữ dữ liệu. Nhưng cũng có các ngoại lệ như: Các index trên các spatial data types sử dụng R-tree; MEMORY table hỗ trợ các hash index; InnoDB sử dụng các inverted list cho FULLTEXT index.

Vậy B-Tree có gì tốt mà lại được MySQL sử dụng cho hầu hết các index như vậy?

B-Tree là cấu trúc dữ liệu dạng cây tự cân bằng.

Nhiều người cho rằng B-Tree là viết tắt của Balanced Tree, tức là cây tự cân bằng.

Nhưng thực tế thì nhóm tác giả tạo ra B-Tree đã từng có câu trả lời chính thức giải thích tại sao họ đặt tên là B-Tree (nó không chỉ đơn thuần có ý nghĩa là "tự cân bằng"):

"So there we were, Rudy and I, at lunch. We had to give the thing a name... We were working for Boeing at the time, but we couldn't use the name without talking to the lawyers. So there's a B.

It has to do with Balance. There's another B.

Rudy was the senior author. Rudy (Bayer) was several years older than I am, and had ... many more publications than I did. So there's another B.

And so at the lunch table, we never did resolve whether there was one of those that made more sense than the rest.

What Rudy likes to say is, the more you think about what the B in B-Tree means, the better you understand B-Trees!"

Mỗi node trong B-Tree có thể chứa nhiều key và nhiều con trỏ đến các node con, giúp giảm độ sâu của cây và tăng tốc độ tìm kiếm.

Tôi sẽ chia thành 2 ý nhỏ để phân tích cho anh em dễ hiểu:

1️⃣ Ý thứ nhất: "Mỗi node trong B-Tree có thể chứa nhiều key"

Chắc anh em đều biết đến cây nhị phân thông thường (Binary Tree) rồi đúng không. Với cây nhị phân thông thường (không cân bằng), các node lá sẽ thường có độ sâu khác nhau. Thế nhưng thực tế là khi phỏng vấn các bạn sinh viên vào vị trí fresher, tôi đã gặp rất nhiều bạn nhầm lẫn B-Tree là Binary Tree thông thường luôn.
Ở cây nhị phân thông thường, anh em sẽ thấy mỗi node chỉ bao gồm 1 số thôi. Node cha sẽ lớn hơn node con bên trái, và nhỏ hơn node con bên phải.
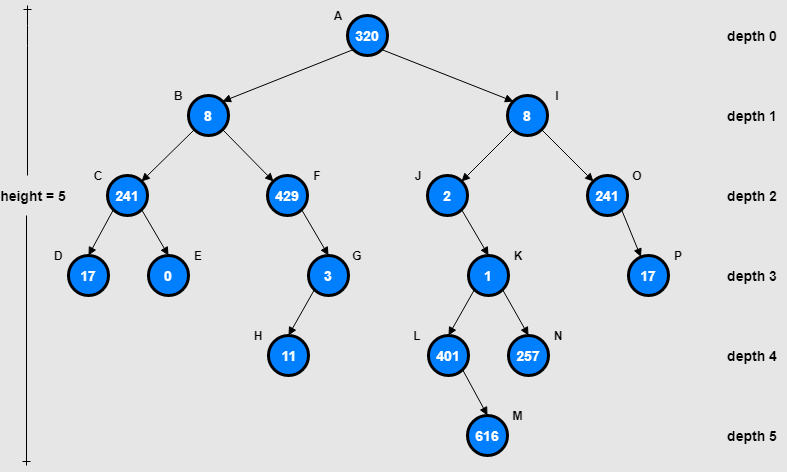
Vậy nếu chúng ta áp dụng cây nhị phân thông thường vào database thì sẽ có thể gặp vấn đề gì?

=> Khi dữ liệu lớn lên, cây nhị phân thông thường sẽ có thể có độ sâu rất lớn (cỡ log₂(N)).

=> Điều này dẫn đến việc mỗi lần tìm kiếm sẽ phải đi qua nhiều node, tức là phải đọc nhiều lần từ ổ cứng.
Vậy khi chuyển sang dùng B-Tree (cây cân bằng) thì sao? Mỗi node của B-Tree có thể chứa nhiều số khác nhau (hay còn gọi là nhiều keys)
Chính vì nhờ tính chất này mà khi dữ liệu lớn lên, cây sẽ có xu hướng "phình ra" theo chiều ngang hơn là chiều sâu.
Độ sâu của B-Tree lúc này chỉ còn là logₘ(N) (với m là số keys tối đa trên 1 node)
Ví dụ:
- Với 1 tỷ keys (1.000.000.000 số), giả sử mỗi node của B-Tree chứa tối đa 1000 keys, thì chúng ta sẽ chỉ cần log₁₀₀₀(1.000.000.000), tức là độ sâu của cây = 3 tầng là đủ.
- Hoặc kể cả trường hợp mỗi node của B-Tree chỉ chứa tối đa 100 keys, thì chúng ta cũng sẽ chỉ cần độ sâu log₁₀₀(1.000.000.000) = khoảng 4 đến 5 tầng.
- Giảm đáng kể số lần đọc dữ liệu từ ổ cứng so với cây nhị phân thông thường. Vì cây nhị phân thông thường khi đó sẽ cần: log₂(1.000.000.000) = 30 tầng.
Đọc đến đây chắc có bạn sẽ đặt câu hỏi ủa tại sao "tìm kiếm sẽ phải đi qua nhiều node" lại liên quan đến việc "phải đọc nhiều lần từ ổ cứng"???
- Lý do là vì ổ cứng (HDD/SSD) không đọc/ghi từng byte riêng lẻ mà đọc/ghi theo khối (block), thường có kích cỡ khoảng 4KB, 8KB, hoặc 16KB.
- Ví dụ: Dù bạn chỉ cần đọc 1 số (ví dụ: số 21), ổ cứng vẫn phải đọc cả block 4KB chứa số đó.
- Đây là đặc điểm vật lý của ổ cứng, khiến việc đọc nhiều block nhỏ liên tiếp trở nên chậm hơn so với việc đọc 1 block lớn.
- Database thì thường xuyên phải đọc dữ liệu từ ổ cứng, vì dữ liệu quá lớn nên KHÔNG THỂ lôi hết lên RAM để xử lý cho nhanh được.
- Mỗi node của B-Tree có kích thước bằng đúng 1 disk block. Khi đọc 1 node, bạn sẽ lấy được nhiều keys cùng lúc (ví dụ: 1000 keys)
- Cây nhị phân thông thường chỉ lưu 1 key trong mỗi node, nên nếu muốn lấy 1000 keys sẽ phải đọc 1000 blocks, trong khi B-Tree chỉ cần đọc 1 block.
- Giả sử, mỗi lần đọc dữ liệu từ ổ cứng tốn ~10ms (với HDD) hoặc ~0.1ms (với SSD):
  - Với cây nhị phân thông thường phải đọc 30 lần cho 1 truy vấn, thời gian sẽ là: (HDD) 30 × 10ms = 300ms; (SSD) 30 × 0.1ms = 3ms.
  - Với B-Tree chỉ cần 3 lần cho 1 truy vấn, thời gian sẽ là: (HDD) 3 × 10ms = 30ms; (SSD) 3 × 0.1ms = 0.3ms.
  => B-Tree giúp database xử lý truy vấn nhanh hơn hàng chục lần, đặc biệt với dữ liệu lớn.

2️⃣ Ý thứ hai: "Mỗi node trong B-Tree có thể có nhiều con trỏ đến các node con"

Với cây nhị phân thông thường, các bạn sẽ thấy mỗi node cha chỉ có tối đa 2 node con chính là 2 số, trong đó số ở node con bên trái nhỏ hơn số ở node cha, còn số ở node con bên phải lớn hơn số ở node cha.
Tuy nhiên đối với B-Tree, một node cha có thể có nhiều hơn 2 node con, vậy nên nó sẽ có nhiều con trỏ hơn để trỏ đến các node con đó.
Vậy anh em sẽ có thể thắc mắc: Một node cha có nhiều hơn 2 node con, hay có nhiều con trỏ hơn để làm gì? Tại sao không dùng ít con trỏ hơn (ví dụ như cây nhị phân thông thường)?
- Thì thực tế câu trả lời cũng tương tự như ở ý thứ nhất thôi.
- Vấn đề của cây nhị phân thông thường là mỗi node chỉ có 2 con trỏ (trái/phải), dẫn đến cây sẽ có độ sâu lớn khi dữ liệu tăng lên. Như ở trên tôi đã phân tích về trường hợp tìm kiếm trên 1 tỷ keys.
- Giải pháp mỗi node có nhiều con trỏ của B-Tree là để khi dữ liệu tăng lên, cây sẽ "phình ra" theo chiều ngang nhiều hơn thay vì chiều sâu. Từ đó giúp giảm số lần đọc dữ liệu từ ổ cứng.

❌ NHƯNG, nếu các bạn từng đọc nhiều bài viết của tôi trước đây thì sẽ thấy tôi rất thích từ "trade-off" hay còn gọi là "đánh đổi"

Khi học lập trình nói chung và làm việc trong lĩnh vực CNTT nói riêng, chúng ta sẽ thấy anh em đồng nghiệp thường xuyên sử dụng từ này.
Không có giải pháp nào là chìa khóa vạn năng và tối ưu trong mọi trường hợp cả.
Đơn giản như việc ngày xưa anh em học thuật toán Bubble sort (sắp xếp nổi bọt), anh em sẽ nhận thấy một số ưu điểm của nó như dễ học, dễ hiểu, dễ cài đặt cho người mới học lập trình. Nhưng nhược điểm lại là tốc độ sắp xếp chậm với độ phức tạp thời gian ở trường hợp xấu nhất và trung bình là O(n²), rất chậm với các mảng lớn chưa được sắp xếp. Đó chính là sự đánh đổi, được cái lọ thì mất cái chai 🤷‍♂️
Và quay lại với cấu trúc dữ liệu B-Tree mà chúng ta đang thảo luận thì cũng vậy thôi.
Mặc dù ở trên các bạn có thể thấy B-Tree có rất nhiều ưu điểm so với cây nhị phân thông thường, đặc biệt là tối ưu hóa cho dữ liệu lớn. Nhưng nếu xem xét kỹ thì thấy nó cũng có những nhược điểm riêng:
- Mỗi node phải sắp xếp các keys theo thứ tự và duy trì con trỏ tương ứng. Node càng nhiều keys thì sẽ càng tốn nhiều dung lượng RAM hơn khi load vào bộ nhớ (nhưng đổi lại thì lại giảm được số lần đọc dữ liệu từ ổ cứng, giúp tiết kiệm thời gian vì đọc từ ổ cứng chậm hơn đọc từ RAM rất nhiều lần) => Đây là sự đánh đổi hợp lý giữa bộ nhớ và tốc độ truy cập.
- Khi thêm/xóa key, cần chia/gộp node để đảm bảo cây cân bằng.
- Một nhược điểm nữa mà tôi cũng đã viết bài ví dụ rất kỹ ở bài trước, đó là B-Tree index sẽ không có hoạt động khi "bạn tạo một composite index ví dụ như CREATE INDEX idx_name ON users (last_name, first_name); nhưng lúc viết câu lệnh truy vấn lại sử dụng sai thứ tự cột trong composite index (ví dụ SELECT * FROM users WHERE first_name = 'Sang';)". Các bạn có thể đọc lại phần "Sai lầm 4: Hiểu sai/Không hiểu về cách hoạt động của Composite Index" ở bài viết trước của tôi nhé.

🤔 Rồi cũng sẽ có bạn hỏi thêm rằng, vậy sao không dùng Hash Index làm chủ đạo, với độ phức tạp thời gian khi thực hiện tìm kiếm là O(1)???

Thì câu trả lời là hash index có thể tìm kiếm rất nhanh khi chúng ta dùng so sánh bằng trong câu truy vấn, nhưng nó lại không hỗ trợ truy vấn theo khoảng giá trị. Ví dụ như SELECT * WHERE age BETWEEN 20 AND 30
Ngoài ra optimizer cũng không thể sử dụng hash index để tăng tốc ORDER BY. Bởi vì chúng ta không thể sử dụng hash index để tìm kiếm entry tiếp theo theo thứ tự.

=> B-Tree được lựa chọn vì sự cân bằng giữa tốc độ và tính linh hoạt của nó.

Các bạn cũng có thể đọc thêm về so sánh giữa B-Tree và Hash Index trong bài viết trên documentation chính thức của MySQL

2. Cấu trúc dữ liệu R-Tree, Hash Index và Inverted List

Ở đầu bài viết tôi cũng đã trích dẫn một đoạn từ documentation của MySQL ghi là:

"Most MySQL indexes (PRIMARY KEY, UNIQUE, INDEX, and FULLTEXT) are stored in B-trees. Exceptions: Indexes on spatial data types use R-trees; MEMORY tables also support hash indexes; InnoDB uses inverted lists for FULLTEXT indexes."

có nghĩa là:

Hầu hết các index trong MySQL (ví dụ như PRIMARY KEY, UNIQUE, INDEX, FULLTEXT) sử dụng cấu trúc dữ liệu B-Tree để lưu trữ dữ liệu. Nhưng cũng có các ngoại lệ như: Các index trên các spatial data types sử dụng R-tree; MEMORY table hỗ trợ các hash index; InnoDB sử dụng các inverted list cho FULLTEXT index.

Ở phần 1 tôi đã phân tích rất kỹ về B-Tree rồi.

Thế nên sang phần 2 này tôi sẽ nói về các trường hợp ngoại lệ.

2.1. Spatial Data Types sử dụng R-tree

Câu hỏi được đặt ra chắc hẳn sẽ là Tại sao Spatial Data Types lại không dùng B-Tree???

B-Tree được thiết kế cho dữ liệu một chiều (ví dụ như dữ liệu số, string, ...), nhưng những dữ liệu dạng spatial (không gian) như tọa độ địa lý, hình học (điểm, đường, đa giác, ...) thì lại có tính chất đa chiều. Trong khi đó R-tree lại là cấu trúc dữ liệu rất phù hợp cho kiểu dữ liệu này.

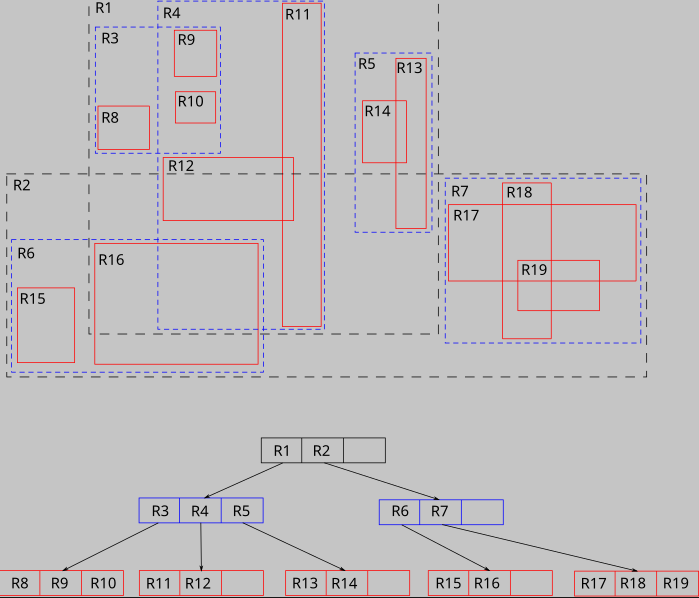
R-tree

RTree-Visualization-3D

Ví dụ:
Ứng dụng bản đồ cần tìm các nhà hàng trong phạm vi 5km quanh vị trí hiện tại. Spatial index sử dụng R-tree sẽ nhanh chóng xác định các đối tượng nằm trong hình tròn (hoặc hình chữ nhật) mà không cần quét toàn bộ dữ liệu.

-- Tạo spatial index trên cột location (kiểu dữ liệu của cột này là GEOMETRY)
CREATE SPATIAL INDEX idx_location ON restaurants(location);

-- Truy vấn tìm nhà hàng trong phạm vi nhất định
SELECT * FROM restaurants 
WHERE ST_Contains(ST_Buffer(@user_location, 5), location);

2.2. `MEMORY` Table hỗ trợ Hash Index

Tương tự như trên, chúng ta sẽ đặt câu hỏi tại sao MEMORY table lại không dùng B-Tree nhỉ???

MEMORY storage engine (trước đây được gọi là HEAP) lưu dữ liệu trên RAM - bộ nhớ truy cập ngẫu nhiên (random access) rất nhanh.
Nhưng đổi lại, nhược điểm của nó là vì lưu trên RAM nên dữ liệu sẽ có thể bị mất khi gặp sự cố phần cứng trên server hoặc đơn giản là ... mất điện. Thế nên MySQL họ cũng khuyến cáo chỉ nên sử dụng các bảng này làm các temporary work areas hoặc read-only caches cho dữ liệu được lấy từ các bảng khác.
Mà hash index lại giúp truy xuất cực kỳ nhanh trong các tình huống đó, vì hash index tối ưu cho tìm kiếm chính xác (exact match) hay hiểu đơn giản là so sánh bằng (=) với độ phức tạp O(1)
Tuy nhiên, như tôi cũng đã phân tích ở phần 1, nhược điểm của hash index là nó không hỗ trợ truy vấn theo khoảng giá trị. Ví dụ như SELECT * WHERE age BETWEEN 20 AND 30. Và nó cũng không hỗ trợ ORDER BY tốt.
Vậy nên, mặc dù hash index được thiết lập mặc định cho MEMORY table, nhưng storage engine này vẫn support B-Tree index nếu bạn muốn. Bạn có thể tạo MEMORY table với USING BTREE

2.3. InnoDB sử dụng Inverted List cho `FULLTEXT` Index

Lý do không dùng B-Tree:

FULLTEXT index được tạo trên các text-based columns (ví dụ như các cột có kiểu dữ liệu là CHAR, VARCHAR, hoặc TEXT) để tăng tốc các truy vấn trên dữ liệu có trong các cột đó. Nó dùng để tìm kiếm dựa trên từ khóa, chứ không phải tìm giá trị chính xác.
Full-text search được thực hiện bằng cú pháp MATCH() ... AGAINST, nó giúp cho chúng ta:
- Tìm xem từ khóa nào xuất hiện trong một đoạn text lớn.
- Có thể tính điểm (relevance score) dựa trên số lần và vị trí xuất hiện.
Việc này không phù hợp với B-Tree, vốn chỉ hoạt động tốt với truy vấn =, BETWEEN, LIKE 'abc%', ...
Trong khi đó, inverted list lưu trữ danh sách các từ (word) và ánh xạ với danh sách các document mà từ đó xuất hiện. Để hỗ trợ proximity search, thông tin vị trí cho mỗi từ cũng được lưu trữ dưới dạng byte offset.
Điều này cho phép truy vấn rất nhanh, tra một từ có thể nhanh chóng ra danh sách document chứa từ đó.

Trên documentation của MySQL có một ví dụ rất dễ hiểu về cách sử dụng của FULLTEXT index và MATCH() ... AGAINST như sau, các bạn có thể tham khảo:

CREATE TABLE opening_lines (
     id INT UNSIGNED AUTO_INCREMENT NOT NULL PRIMARY KEY,
     opening_line TEXT(500),
     author VARCHAR(200),
     title VARCHAR(200),
     FULLTEXT idx (opening_line)
     ) ENGINE=InnoDB;

BEGIN;

INSERT INTO opening_lines(opening_line,author,title) 
VALUES ('Call me Ishmael.','Herman Melville','Moby-Dick'), 
('A screaming comes across the sky.','Thomas Pynchon','Gravity Rainbow'), 
('I am an invisible man.','Ralph Ellison','Invisible Man'), 
('Where now? Who now? When now?','Samuel Beckett','The Unnamable'), 
('It was love at first sight.','Joseph Heller','Catch-22'), 
('All this happened, more or less.','Kurt Vonnegut','Slaughterhouse-Five'), 
('Mrs. Dalloway said she would buy the flowers herself.','Virginia Woolf','Mrs. Dalloway'), 
('It was a pleasure to burn.','Ray Bradbury','Fahrenheit 451');

SELECT COUNT(*) FROM opening_lines WHERE MATCH(opening_line) AGAINST('Ishmael');
+----------+
| COUNT(*) |
+----------+
|        0 |
+----------+

COMMIT;

SELECT COUNT(*) FROM opening_lines WHERE MATCH(opening_line) AGAINST('Ishmael');
+----------+
| COUNT(*) |
+----------+
|        1 |
+----------+

3. Kết luận

Tóm lại, khi so sánh B-Tree với các loại cấu trúc dữ liệu khác được sử dụng để đánh index trong MySQL thì:

So sánh B-Tree với các loại cấu trúc dữ liệu khác

Có thể thấy, mặc dù hầu hết các loại index trong MySQL sử dụng cấu trúc dữ liệu B-Tree, nhưng MySQL vẫn linh hoạt cho phép chúng ta sử dụng các loại cấu trúc dữ liệu khác để đáp ứng đa dạng bài toán, thay vì chỉ dựa vào một mình B-Tree.

Cảm ơn anh em nhiều!

Hẹn gặp lại anh em ở các bài viết tiếp theo trong Series Index nâng cao: Kiến trúc và Tối ưu hóa Index trong MySQL dành cho Developer và DBA 👋

🙋🏻‍♂️ Một số kênh mạng xã hội khác mà tôi dùng để chia sẻ và trao đổi với anh em kiến thức về ngành CNTT và lập trình:

Group "Khi nào giỏi lập trình thì đổi tên 🫢": https://www.facebook.com/groups/gioilaptrinhthidoiten
Page "CLB Lập trình - THPT Ngọc Tảo": https://www.facebook.com/clb.it.ngoctao/
TikTok "CLB Lập trình - THPT Ngọc Tảo": https://www.tiktok.com/@clb.it.ngoctao/
Youtube "Tờ Mờ Sáng học Lập trình": https://www.youtube.com/@tmsanghoclaptrinh/

Database index b-tree tối ưu sql

Mục lục

1. Cấu trúc dữ liệu B-Tree

Vậy B-Tree có gì tốt mà lại được MySQL sử dụng cho hầu hết các index như vậy?

1️⃣ Ý thứ nhất: "Mỗi node trong B-Tree có thể chứa nhiều key"

2️⃣ Ý thứ hai: "Mỗi node trong B-Tree có thể có nhiều con trỏ đến các node con"

2. Cấu trúc dữ liệu R-Tree, Hash Index và Inverted List

2.1. Spatial Data Types sử dụng R-tree

2.2. MEMORY Table hỗ trợ Hash Index

2.3. InnoDB sử dụng Inverted List cho FULLTEXT Index

3. Kết luận

Hẹn gặp lại anh em ở các bài viết tiếp theo trong Series Index nâng cao: Kiến trúc và Tối ưu hóa Index trong MySQL dành cho Developer và DBA 👋

🙋🏻‍♂️ Một số kênh mạng xã hội khác mà tôi dùng để chia sẻ và trao đổi với anh em kiến thức về ngành CNTT và lập trình:

Mục lục

2.2. `MEMORY` Table hỗ trợ Hash Index

2.3. InnoDB sử dụng Inverted List cho `FULLTEXT` Index