Sự Thật Trần Trụi Về Vector Search: Tại Sao Model Lớn Nhất Cũng Sẽ Đầu Hàng
Bạn nghĩ rằng cứ dùng model embedding xịn nhất, to nhất là hệ thống RAG của bạn sẽ thông minh? Bạn đã nhầm.
Trong thế giới hào nhoáng của AI, chúng ta được nghe một lời hứa hẹn: biến mọi thứ thành vector, và bạn sẽ có được một "bộ não" có thể hiểu và tìm kiếm bất cứ thứ gì. Một lời hứa về một không gian ngữ nghĩa nơi mọi khái niệm, dù phức tạp đến đâu, cũng có thể được định vị và truy xuất.
Đó là một câu chuyện hay. Nhưng đó không phải là toàn bộ sự thật.
Có một bí mật bị che giấu, không phải trong thuật toán, mà trong chính nền tảng toán học của embedding. Một giới hạn trần trụi, lạnh lùng mà không một model nào, dù có 4096 hay 8192 chiều, có thể vượt qua.
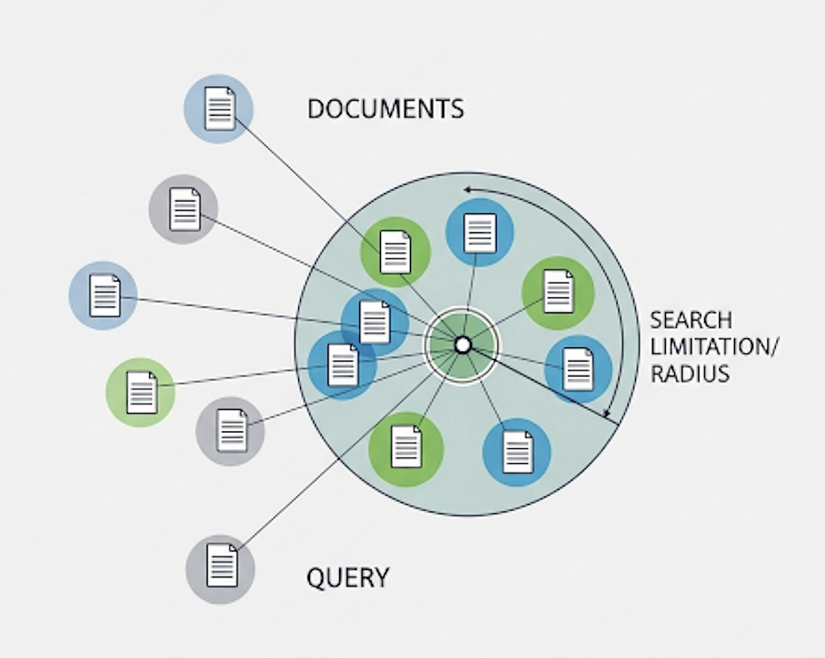
Vết Nứt Đầu Tiên: Khi "Thông Minh" Trở Nên Ngớ Ngẩn
Mọi chuyện bắt đầu khi bạn nhận ra hệ thống của mình, dù được trang bị model hàng tỷ tham số, lại thất bại ở những truy vấn tưởng chừng đơn giản. Nó có thể tìm "tiểu thuyết của George Sand", nhưng lại "bối rối" khi bạn yêu cầu "tiểu thuyết từ năm 1849 HOẶC tiểu thuyết của George Sand".
Tại sao? Chúng ta vẫn nghĩ đó là do model "chưa đủ hiểu". Sự thật thì tàn nhẫn hơn nhiều: model của bạn không phải không hiểu, mà là nó "không thể" biểu diễn được câu trả lời.
Mỗi truy vấn không chỉ đòi hỏi tìm một điểm trong không gian vector, mà là trả về một tập hợp các điểm (tài liệu). Và đây là cú sốc: số lượng các tập hợp khác nhau mà một không gian d chiều có thể trả về là có hạn. Khi bạn bắt đầu dùng các toán tử logic (AND, OR, NOT) hoặc các chỉ dẫn phức tạp, số tổ hợp cần biểu diễn bùng nổ vượt xa khả năng của vector.
Bằng Chứng Tội Phạm: Bộ Dataset LIMIT
Nếu vẫn còn nghi ngờ, hãy nhìn vào LIMIT – một bộ dataset được Google DeepMind tạo ra không phải để thử thách trí thông minh, mà để vạch trần giới hạn của vector.
Nhiệm vụ cực kỳ đơn giản:
Hỏi: "Ai thích Quokkas?"
Đáp: "Jon Durben thích Quokkas và Táo."
Đây là bài toán mà bất kỳ ai cũng nghĩ AI có thể giải quyết dễ dàng. Nhưng kết quả là một thảm họa:
-
Các model embedding SOTA nhất thất bại thảm hại, chỉ đạt dưới 20% recall@100.
-
Ngay cả khi thu nhỏ bộ dữ liệu xuống chỉ còn 46 tài liệu, chúng vẫn không thể giải quyết trọn vẹn.
LIMIT đã chứng minh một điều: vấn đề không nằm ở độ khó của ngôn ngữ, mà ở "mật độ quan hệ" phức tạp mà các model được yêu cầu phải nhồi nhét vào một không gian vector hữu hạn.
Giải Mã Bí Ẩn: Lời Thú Tội Của Toán Học
Thủ phạm chính là Sign Rank và chiều không gian (dimension).
Hãy tưởng tượng không gian vector d chiều của bạn là một tấm bản đồ. Mỗi tài liệu là một thành phố. Khả năng của model là vẽ ra các con đường để từ một điểm (câu hỏi) có thể đến được đúng các thành phố cần thiết (tài liệu liên quan).
Vấn đề là, với một số lượng thành phố nhất định, sẽ có những tập hợp thành phố mà bạn không thể nào vẽ được một con đường duy nhất đi qua tất cả chúng mà không đi nhầm vào những thành phố khác. Tăng dimension (d) chỉ giống như cho bạn thêm một chiều không gian để vẽ đường (từ 2D lên 3D), nó giúp được nhiều hơn, nhưng vẫn không phải là vô hạn.
Nghiên cứu chỉ ra, ngay cả trong điều kiện tối ưu nhất, một model 1024 chiều cũng sẽ "gãy" khi số lượng tài liệu và các mối quan hệ của chúng vượt qua một ngưỡng tới hạn (khoảng 4 triệu tài liệu cho bài toán đơn giản nhất). Con số này chỉ là hạt cát so với kho dữ liệu thực tế.
Lối Thoát Nào Cho Chúng Ta?
Khi bức tường lý thuyết đã quá rõ ràng, việc cố đấm ăn xôi với single-vector là vô ích. Cuộc chơi giờ đây là sự đánh đổi:
-
Quay về với "Kẻ Lỗi Thời" (BM25): Các mô hình sparse như BM25 đột nhiên tỏa sáng trên LIMIT. Tại sao? Vì chúng hoạt động trong một không gian có số chiều cực lớn (bằng kích thước từ vựng). Chúng có đủ "không gian" để biểu diễn, nhưng lại yếu về mặt ngữ nghĩa thuần túy.
-
Chấp Nhận Sự Phức Tạp (Multi-vector & ColBERT): Thay vì một vector cho một tài liệu, hãy dùng nhiều vector. Kiến trúc này tỏ ra hiệu quả hơn đáng kể, nhưng cũng đánh đổi bằng sự phức tạp và chi phí tính toán.
-
Dùng "Vũ Khí Hạng Nặng" (Cross-Encoders): Đây là giải pháp tối thượng về độ chính xác, có thể giải quyết LIMIT một cách hoàn hảo. Nhưng chúng quá chậm và tốn kém, không thể dùng để tìm kiếm trên quy mô lớn.
Đã Đến Lúc Ngừng Mơ Mộng
Ngành retrieval đang đứng trước một ngã ba. Lời hứa về một vector duy nhất có thể giải quyết mọi thứ đã đến hồi kết.
Lần tới, khi bạn xây dựng một hệ thống tìm kiếm và nó trả về những kết quả vô lý, đừng vội đổ lỗi cho dữ liệu hay việc fine-tune. Hãy tự hỏi: "Liệu mình có đang yêu cầu nó làm một điều bất khả thi về mặt toán học không?"
Cuộc chơi không chỉ là về "ngữ nghĩa". Nó là về việc tôn trọng những giới hạn trần trụi của không gian và chiều. Và người chiến thắng sẽ là người hiểu rõ luật chơi này nhất.
Tài liệu tham khảo:
All rights reserved